Постоянная, которую не рассчитывал Лошмидт
Статья Лошмидта «О размерах молекул воздуха» была опубликована в 1865 году в журнале «Sitzungsberichte der kaiserlichen Akademie der Wissenschaften Wien». Он исходил из кинетической теории газов и плотности жидкого воздуха. Однако впервые жидкий воздух был получен Луи Кальете и независимо Раулем Пикте лишь в 1877 году, поэтому Лошмидту пришлось оценивать нужную величину, исходя из свойств других веществ, известных и в виде жидкости, и в виде газа. Как он это сделал?
В газах расстояние между молекулами намного превышает их диаметр. Если считать молекулы сферами и пренебречь притяжением, то можно вычислить давление, теплопроводность, скорость звука, среднюю скорость молекул и кинетическую энергию; это сделали Рудольф Клаузиус, Джеймс Максвелл и Оскар Мейер. Однако размер молекул они не обсуждали.
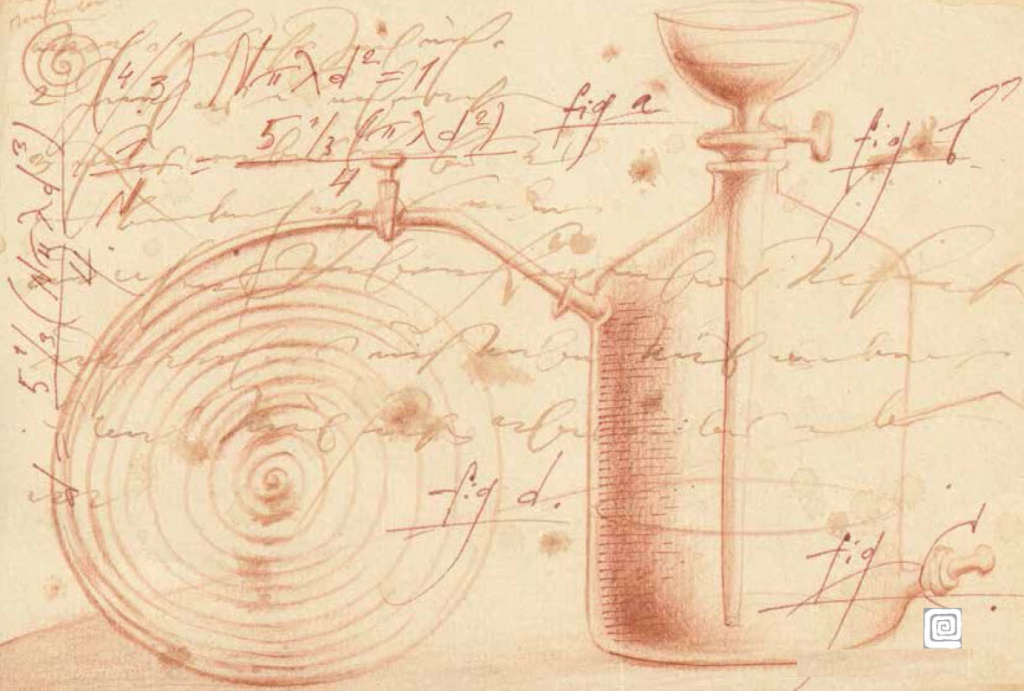
В 1860 году Максвелл, исходя из кинетической теории газов, вывел формулу, которую Клаузиус модифицировал и представил в виде (4/3)Npld2 = 1, где N — число молекул в единице объема (1 см3), l — средний свободный пробег молекул между столкновениями, d — диаметр молекул. Величину 1/N (объем, приходящийся в газе на одну молекулу) Лошмидт назвал «молекулярным объемом газа» и написал: 1/N = 5⅓(pld2)/4. Отсюда для диаметра молекулы получаем d = 5⅓(Npld3)/4 = 8×Npld3/6. Поскольку объем одной молекулы равен pd3/6, величина Npd3/6 равна объему N молекул, находящихся в непосредственном контакте. Назовем объем, фактически занимаемый молекулами в 1 см3 газа, коэффициентом конденсации газа e. Тогда диаметр молекулы связан с коэффициентом конденсации соотношением d = 8el. То есть диаметр молекулы в восемь раз больше среднего свободного пробега, умноженного на коэффициент конденсации. Этот коэффициент можно в первом приближении оценить, разделив объем жидкости на объем того же количества газа, который значительно больше. Объемом пространства между молекулами в жидкости допустимо пренебречь. Этот свободный объем зависит от упаковки молекул. При плотной упаковке сфер они занимают лишь немногим больший объем (примерно в 1,17 раза), чем следует из коэффициента конденсации, но при наиболее свободной упаковке различие возрастает до 1,91. Для несферических молекул верхняя оценка будет больше. Лошмидт использовал неверный коэффициент упаковки шаров 0,855, тогда как он равен 0,740, однако это не изменяет существенно сделанных им выводов.
Можно также предположить, что, когда в жидкости молекулы касаются друг друга, расстояние между их центрами такое же, как при столкновении этих молекул в газе. На это указывает малая сжимаемость жидкостей. Лошмидт применил при расчетах известные из литературы коэффициенты конденсации (отношение мольного объема жидкости к мольному объему идеального газа при нормальных условиях; в скобках даны современные значения), например: Н2О — 0,00081 (0,000803), NO — 0,00154 (0,00133), NH3 — 0,00102 (0,00111), CO2 — 0,00204 (0,00178). Жидкого воздуха в 1865 году, как мы упоминали, еще не получили, плотность его была неизвестна, однако только для воздуха имелись сравнительно надежные данные по величине l. Поэтому Лошмидту нужно было определить e, для чего он использовал аддитивный метод, разработанный немецким химиком Германом Коппом: плотность жидкости рассчитывается как сумма вкладов каждого атома в молекуле. Сам Копп рассчитывал эмпирические константы для вещества на основании опытов, которые проводил с 1841 года. Лошмидт модифицировал константы Коппа; так, для атома С он получил вклад, равный 14 см3/моль, для N — 12 см3/моль в оксидах и 14 см3/моль в цианогруппе и т. д. Лошмидт провел подобные расчеты, воспользовавшись литературными данными для 109 соединений, в основном органических, чтобы показать адекватность модели аддитивных вкладов.
Предположив, что вклады азота и кислорода в воздухе аддитивны (как будто это одно вещество состава N77O23), а также зная отношение плотностей воды и воздуха, Лошмидт для коэффициента конденсации воздуха получил значение 0,000866. Чтобы рассчитать диаметр молекул, нужно знать их средний свободный пробег. Эту величину (0,062 мкм) вычислил в 1860 году Максвелл, исходя из коэффициента вязкости воздуха, измеренного Стоксом. Лошмидт принял l = 0,140 мкм (современное значение для азота 0,0654 мкм). Из этих данных можно было оценить диаметр молекул воздуха: d = 8 · 0,000866 · 0,140 = 9,70 · 10–4 мкм = 0,97 нм. Как писал Лошмидт, «круглым счетом одна миллионная миллиметра, что является лишь грубым приближением, которое, однако, не должно отличаться от истинного более, чем на порядок величины». Действительно, современное число для молекул азота и кислорода всего в три раза меньше. А если бы Лошмидт применил для среднего свободного пробега более правильные данные Максвелла, определил бы d = 8 · 0,000866 · 0,062 = 4,3 · 10–4, лишь на 30% больше правильного значения.
В заключение Лошмидт рассуждает о смысле полученных им оценок. Он указывает, что как километр — подходящая единица для самых больших расстояний на Земле, так миллионная часть миллиметра (примерно 1/700 длины волны красного света) выражает размеры в царстве атомов и молекул. При этом молекулы, содержащиеся в объеме 1 мм3, на плоскости займут площадь 1 м2! Лошмидт также рассуждает о размерах биомолекул, клеточных мембран и т. д. Но самое удивительное, что он идет дальше и говорит о возможности рассматривать атомы, например, водорода и кислорода, как «конгломераты многих более мелких частиц» — за 32 года до открытия электрона и за 44 года до открытия атомного ядра!
А где же ставшее знаменитым «число Лошмидта» (оно же постоянная Лошмидта), то есть число молекул в единице объема? В статье о нем нет ни слова! Хотя в Большой Советской энциклопедии написано: «Лошмидт... впервые определил число молекул в единице объема газа, исходя из кинетической теории газов (1865)». Однако не было этого. А ведь Лошмидт легко мог бы рассчитать «свою» постоянную, у него были все необхожимые данные. Из формулы Максвелла — Клаузиуса 1 = (4/3)Npld2 не трудно определить число частиц в 1 см3: N = 3/(4pld2) = 3/[(4 ´ 3,14 × 0,140.10–4 см × (9,7.10–8 см)2] = 0,18.1020 = 1,8.1019 см–3. Это довольно близко к значению, которое может рассчитать любой школьник из постоянной Авогадро и мольного объема идеального газа: 6,02.1023/22400 см3 ≈ 2,7.1019 см–3. Возникают два вопроса: почему Лошмидт не провел этот расчет и почему постоянная носит его имя? На первый вопрос можно ответить предположительно: потому что Лошмидту было неинтересно, сколько молекул в 1 см3. Второй вопрос связан, как написал полвека назад историк химии Роберт Хоторн, с «вековой тайной».
В том же 1865 году, когда Лошмидт опубликовал свою статью, в журнале «Zeitschrift für Mathematik und Physik» появилось краткое, на двух страничках, изложение статьи Лошмидта, в начале которого стоит его фамилия и в котором приводится то, что мы называем «постоянной Лошмидта». Однако есть несколько причин, по которым Лошмидт не может быть автором этого фактически развернутого реферата. Приведенное в той статье число молекул в 1 мм3 (8,66.1017) не согласуется со значением, которое можно получить из статьи Лошмидта. В этом обзоре немало и других ошибок, например, для среднего свободного пробега дано значение 0,170 мкм (вместо 0,140 у Лошмидта), для диаметра молекулы 11,7 · 10–4 мкм (у Лошмидта 9,70 · 10–4 мкм), при этом перепутаны обозначения диаметра и среднего свободного пути. Наконец, носители немецкого языка утверждают, что стиль этого изложения совершенно не соответствует стилю статей Лошмидта. По всей вероятности, реферат был кем-то небрежно подготовлен, но именно в нем впервые появилось число молекул газа в единице объема, которое впоследствии получило название «постоянная Лошмидта».