Полку матрешек прибыло
До сих пор углеродные матрешки (рис. 1) делали из идеальных фуллеренов, вкладывая их друг в друга (эндоэдральный комплекс).
 |
|
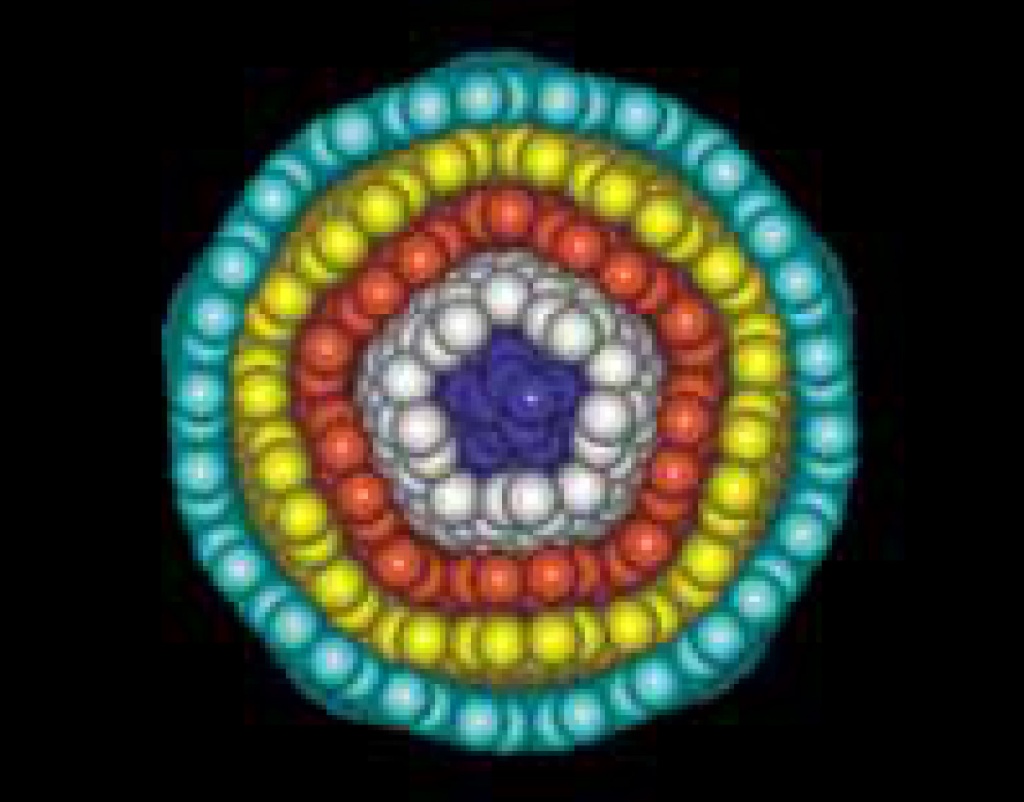
1. Срез матрешки из идеальных фуллеренов С1500, С960, С540, С240 и С60
|
Заметим, что на поверхности таких фуллеренов 12 пятичленных циклов равномерно распределены по одному среди (N–20)/2 шестичленных циклов (N — число атомов углерода). В результате получается замкнутая поверхность икосаэдрической формы.
Нам удалось расширить круг материала для матрешек, собрав модели углеродных октаэдров и тетраэдров (рис. 2).
 |
|
2. Углеродные октаэдр С3860 (а) и тетраэдр С2672 (б). Ребра окрашены, чтобы подчеркнуть объем
|
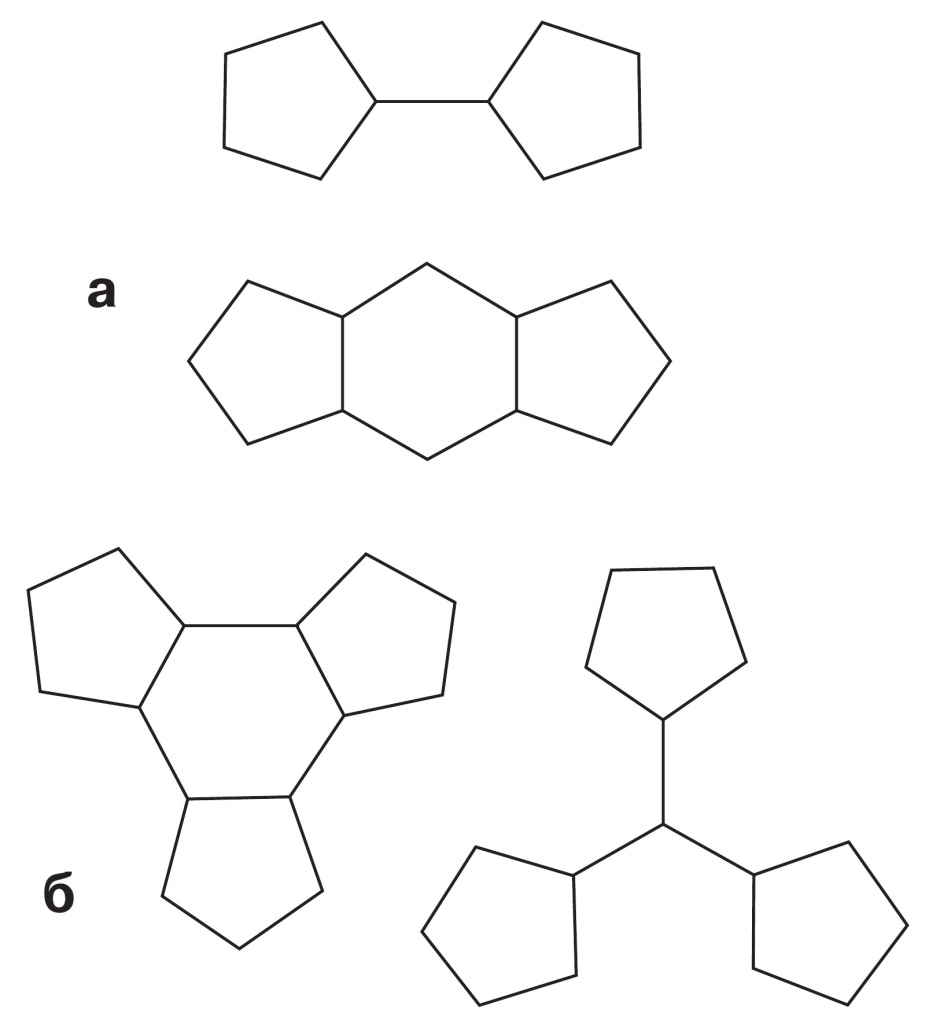
По сути, углеродный октаэдр — это тот же фуллерен, просто у него 12 пятичленных циклов расположены иначе: на закругленных вершинах углеродной поверхности сгруппированы по два пятичленных цикла (рис. 3а), равномерно распределенных среди (N–20)/2 шестичленных циклов. Получается замкнутая поверхность октаэдрической формы.
 |
|
3. Расположение пятичленных циклов в вершинах углеродных октаэдра (а) и тетраэдра (б)
|
Если двенадцать пятичленных циклов сгруппировать по три (рис. 3б), то вместе с (N–20)/2 шестичленными циклами они образуют замкнутую тетраэдрическую поверхность (рис. 2б).
На рис. 4 показаны срезы матрешки из трех эндоэдральных углеродных октаэдров. Их размеры подобраны с таким расчетом, чтобы расстояние между ближайшими поверхностями было того же порядка (0,33—0,35 нм), что и в графите. При этом между соседними октаэдрами возникает заметное взаимодействие, вследствие чего эндоэдральный комплекс оказывается энергетически выгоднее, чем три отдельно взятых углеродных октаэдра.
 |
|
4. Срезы матрешки из углеродных октаэдров С3860, С2876 и С2036. Раскраска «внутренности» модели сделана для большей наглядности
|
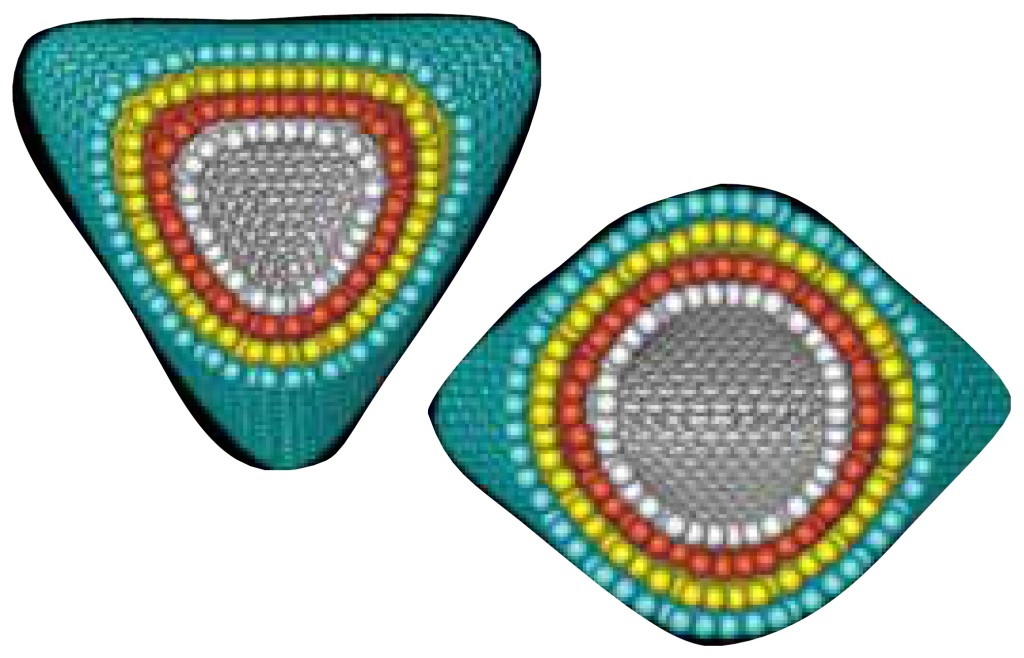
На рис. 5 показаны срезы матрешки из четырех углеродных тетраэдров, которым также энергетически выгоднее быть вместе, чем в отдельности.
 |
|
5. Срезы матрешки из углеродных тетраэдров С2672, С2272, С1568 и С1264
|
Таким образом, замкнутые высокосимметричные углеродные поверхности могут иметь не только форму тела Архимеда — усеченного икосаэдра (классические идеальные фуллерены), но и форму тел Платона — тетраэдра и октаэдра, которые также допускают объединение в эндоэдральные комплексы — матрешки.
Еще одно платоново тело, куб, не может служить заготовкой для углеродной поверхности и матрешек, которые сохраняли бы симметрию куба, так как распределить поровну 12 пятичленных циклов между 8 вершинами невозможно.
Закономерный вопрос: известно ли что-то о существовании в природе октаэдрического и тетраэдрического углерода, матрешек из них, где их искать и как можно было бы идентифицировать? Отвечаем: неизвестно, ведь сама идея таких форм углерода возникла совсем недавно. Искать нужно в фуллереновой саже или в самом обычном графите путем (с помощью) сканирования и анализа электронных микрофотографий, создания доступной базы этих данных, сравнения со срезами компьютерных моделей. Возможно, как делают в астрономии, стоило бы привлечь к этому делу молодых любителей, стремящихся наблюдать и открывать новое и неизведанное.
Доктор химических наук
М.Ю. Корнилов
