Раша, куда ж несешься ты? дай ответ! не дает ответа...

В официальных документах, относящихся к ЕГЭ, отсутствует описание методов обработки его результатов. Вместо этого приводятся лишь ссылки на научные публикации, содержащие их обоснование. Возьмем на себя труд хотя бы в общих чертах реконструировать процесс пересчета первичных баллов в тестовые.

В основе лежит однопараметрическая модель Раша, формулирующаяся для заданий с дихотомическим исходом (успех/неуспех). Она сводится к гипотезе о том, что отношение вероятности справиться с некоторым заданием p к вероятности не справиться с ним 1-p равно отношению знаний испытуемого Z к трудности этого задания T. Две последние величины сами по себе неопределимы, и возможно оперировать только их отношением. Поэтому, как это часто делается в подобных случаях, переходят к логарифмической мере — логитам знаний z = ln Z/W и трудностей t = ln T/W, где W — некий опорный уровень знаний и трудностей (его выбор, равно как и выбор основания логарифма, несуществен, поскольку линейное отображение диапазона логитов знаний на заранее определенный диапазон тестовых баллов элиминирует эти два параметра).

Результат выполнения задания характеризуется величиной a, равной единице в случае успеха и нулю в случае неуспеха. Если испытуемому, имеющему знания z, предложено задание трудности t, то вероятность исхода a в соответствии с моделью Раша есть

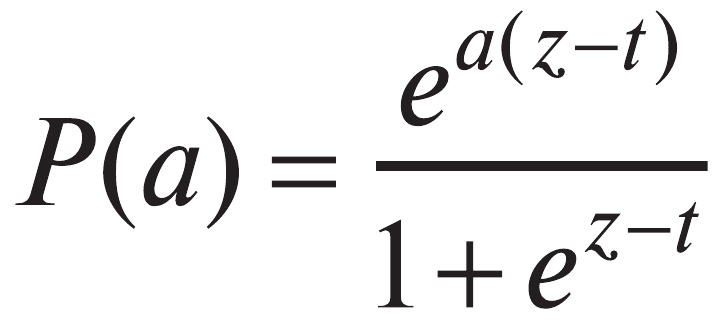
На основе этой формулы можно построить методику обработки результатов экзамена. Для простоты рассмотрим случай единственного варианта заданий.

Пусть имеется N испытуемых, обладающих знаниями z_i (i = 1,2,…N), и каждому из них предложены K заданий сложностей t_j (j = 1,2,…K). Результатом тестирования будет матрица исходов ||a_ij|| размерности NxK. Для нахождения на ее основе неизвестных величин z_i и t_j/sub> используется метод наибольшего правдоподобия. Он требует максимизации произведения вероятностей полученных исходов P_ij(a_ij):

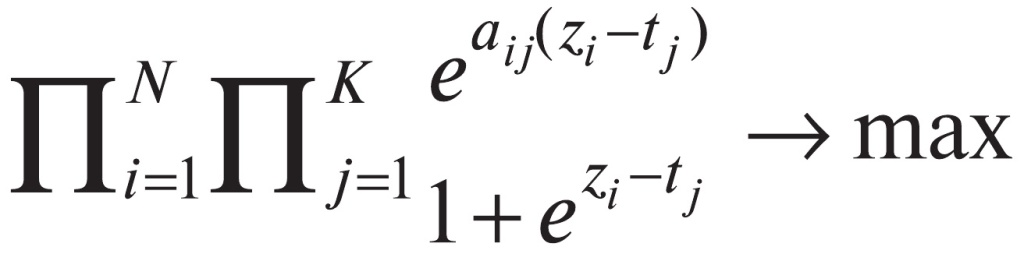
что приводит к системе N+K уравнений:

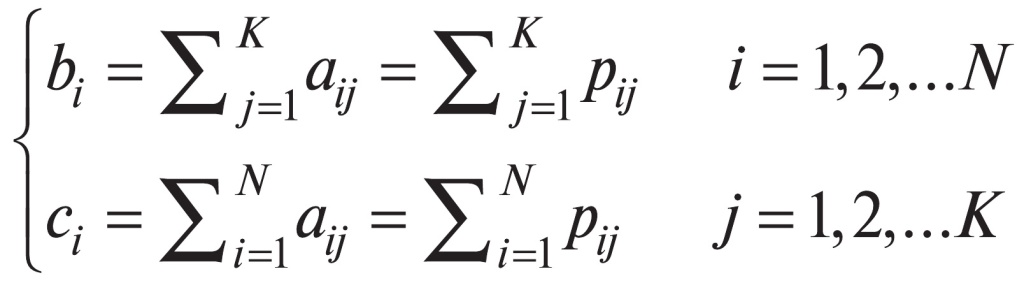
где

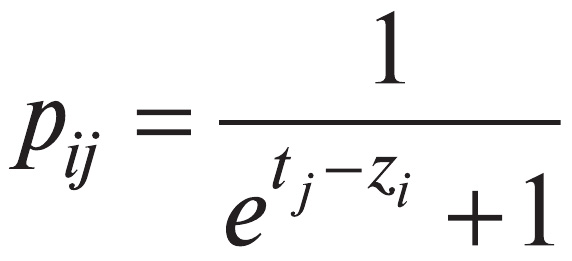
есть вероятность успешного выполнения задания j экзаменуемым i.

Таким образом, требуется совпадение суммы исходов по всем заданиям (первичного балла экзаменуемого b_i) и суммы исходов по всем экзаменуемым (первичного балла задания c_j) с суммами соответствующих вероятностей успеха.

В результате решения данной системы уравнений каждое задание получает оценку трудности t_j, которая далее, скорее всего, используется только для соотнесения трудности разных вариантов и в случае единственного варианта не используется вовсе, а каждый экзаменуемый — оценку знаний z_i, которая, однако, сама по себе тоже не может быть использована. Дело в том, что экзаменуемые, получившие одинаковый первичный балл b_i, могли набрать его на заданиях разной трудности, что выльется для них в разные оценки знаний z_i. Однако процедура вычисления последних полностью сокрыта, и невозможно доказать отсутствие ошибки или обмана. Поэтому с 2008 года была введена дополнительная стадия осреднения. Сначала для каждого значения первичного балла b_i вычисляется среднее значение знаний z_i по всем экзаменуемым, набравшим такой первичный балл, которое считается оценкой их подготовленности. Далее эти оценки линейным образом масштабируются так, чтобы диапазон их изменения простирался от 0 до 100. Это и будут тестовые баллы.

Есть и еще один подводный камень: для экзаменуемых, показавших абсолютный результат (все или ничего), модель Раша дает оценку подготовленности z = ±∞. Однако линейно отобразить неограниченный диапазон знаний на ограниченный диапазон тестовых баллов невозможно. Поэтому при наличии экзаменуемых, осиливших все задания или не осиливших ни одного, процедура масштабирования в принципе невыполнима. Остается невыясненным, как эта трудность преодолевалась ранее, но в 2008 году правило расчета тестовых баллов было скорректировано. Нулевому результату теперь соответствуют 0 тестовых баллов, стопроцентному — 100, а вот уже остальные оценки подвергаются линейному отображению на диапазон от 6 до 94 баллов. Почему минимальное отклонение от абсолютного результата составляет именно 6 баллов, причем для всех предметов, неизвестно.

Реально на экзамене предлагаются задания не с дихотомическим, а с политомическим исходом, то есть оцениваемые не из одного, а из нескольких первичных баллов. Для обработки результатов выполнения таких заданий используется одно из расширений модели Раша, называемое Partial Credit Model. Эта модель опирается на гипотезу, что отношение вероятности p_k набрать k баллов при выполнении некоторого задания к вероятности p_k-1 набрать k-1 балл равно отношению знаний экзаменуемого Z к трудности получения k-го балла T_k этого задания. Иными словами, базовая формула модели Раша

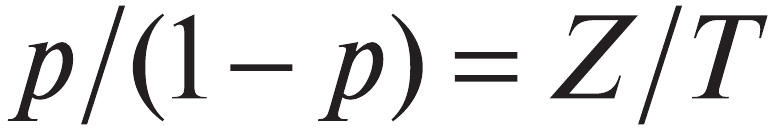
заменяется более общим предположением

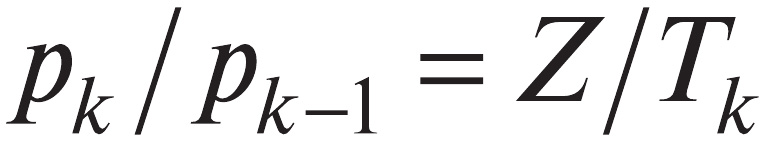
включающим ее в себя как частный случай.

Весь дальнейший анализ для Partial Credit Model осуществляется точно так же, как и для модели Раша. Однако результирующие формулы при этом получаются крайне громоздкие, поэтому мы их не приводим.