Механика мягкой силы
 |
|
Изображение: hu.gatech.edu
|
В научной практике редко бывает так, чтобы автор работы, отмеченной высшей наградой, второй раз получил ту же награду за продолжение исследования. Как правило, если Нобелевскую премию и дают повторно, то по другому поводу. Например, Мария Склодовская-Кюри получала Нобелевскую премию по физике за исследование радиации и по химии — за открытие радия, Лайнус Полинг — по химии за изучение природы химической связи и премию мира за борьбу с распространением ядерного оружия. Комитет экспертов Игнобелевской премии может в 2017 году создать прецедент. Дело в том, что лауреаты премии 2015 года по физике провели новое исследование схожей проблемы, которое просто не может не принести им повторного лауреатства в той же номинации. Если два года назад они объяснили, почему любое млекопитающее крупнее крысы опорожняет мочевой пузырь в среднем за 21 секунду («Proceedings of the National Academy of Science» - полный текст), то в этом году получен ответ на вопрос, почему твердые экскременты выходят из млекопитающего за 12 секунд («Soft Matter»).
Как ни странно, до недавнего времени такие важнейшие процессы, как избавление организма от продуктов жизнедеятельности, то есть деуринация и дефекация, были описаны скорее феноменологически. Исследовали механические, физико-химические характеристики выделяемых веществ, как-то их классифицировали, изучали строение органов выделения, однако никакой математической теории, позволяющей перевести описание этих процессов под юрисдикцию точных наук, построено не было. Хотя, казалось бы, особых затруднений это не должно вызвать — в первом случае действует гидродинамика, а во втором — механика деформируемых сред: науки, хорошо разработанные. Но вот в 2014 году ситуация изменилась: студенты из лаборатории доцента Дэвида Л. Ху в Технологическом университете Джорджии при поддержке грантов для молодых специалистов Национального научного фонда США и Президента университета взялись создать такую модель.
Исследователи начали свой тернистый путь к славе с простейшего вида работы — наблюдения за соответствующим процессом у разных животных. Для этого они снимали на видеокамеру акты испражнения обитателей зоопарка Атланты, а также пользовались видеороликами из Сети. Довольно скоро в наблюдениях стала прослеживаться система. Так, оказалось, что существуют два механизма избавления организма от отработанной жидкости. Маленькие животные, весом до 0,3 кг, делают это капельками, а большие животные — струйкой или струей, в зависимости от размера. На этом-то этапе и была установлена удивительная закономерность, которая принесла участникам работы почетный нанограмм золота: время испражнения у крупных животных оказалась константой, не зависящей от веса: 21 ± 13 секунд. Причем различие в размерах огромно: у кота объем мочевого пузыря в 3600 раз меньше, чем у слона! Казалось бы, слону нипочем кота не догнать. Как же это ему удается?
Для поиска ответа была построена ставшая знаменитой математическая модель. Вот ее краткое описание. Представим, что по трубе, длина и диаметр которой соответствуют таковым у мочеиспускательного канала животного, течет поток жидкости. Его движению способствуют две силы: давление мочевого пузыря и сила тяжести, а замедляют его вязкость, сила инерции и капиллярная сила. Сила давления пузыря удивительным образом представляет собой фундаментальную физиологическую константу: как показали измерения, проведенные зоологами, у млекопитающих оно составляет примерно 5,2 кПа независимо от размеров. Гравитационная сила, она же гидростатическое давление, пропорциональна длине трубы. Сила инерции или динамическое давление — квадрату скорости потока. Сила вязкого давления — квадрату скорости потока и отношению длины трубы к ее диаметру. А капиллярная сила, стремящаяся свернуть струю в капли, — обратно пропорциональна диаметру трубы. Для больших животных остаются первые три силы, а вязкостью и капиллярной можно пренебречь. Тогда получится уравнение, в котором скорость потока выражена через параметры трубы и давление пузыря. Подставив этот результат в формулу для вычисления времени опорожнения мочевого пузыря, получаем зависимость от его объема и опять же параметров трубы. И все они, оказывается, закономерным образом зависят от веса тела. Так, объем пропорционален весу в первой степени, а длина и диаметр мочеиспускательного канала — кубическому корню из веса. Подстановка этих зависимостей в формулу для времени показывает, что оно пропорционально весу в степени 1/6 или примерно 0,16, то есть зависимость от веса все-таки есть, но очень слабая. В общем-то точный расчет времени по экспериментальным данным дает не совсем константу, а именно слабую зависимость — с показателем 0,13. Такое совпадение свидетельствует: модель очень хороша. Из нее становится ясно, почему кот и слон освобождаются от жидкости за одно время, — у слона всё больше: и пузырь, и длина канала, и его диаметр. В результате выше вклад силы тяжести, которая увеличивает скорость истечения потока, это и позволяет слону догнать кота в заочном соревновании.
А вот с мышами и крысами все сложнее. У них преобладают три силы: давление пузыря, вязкое давление и капиллярные силы, они дают сильную нелинейность зависимостей. В результате простую формулу вывести не получается, никаких инвариантов выявить не удается. Это соответствует эксперименту: времена мочеиспускания мелких животных различаются двадцатикратно, от 0,1 до 2 секунд! Модель позволила рассчитать и минимальное животное, способное самостоятельно избавляться от мочи: у него диаметр канала равен 100 мкм. Это соответствует длине канала в 1,7 мм и весу в 0,8 г. Таковы параметры новорожденных мышат: их вес 0,5—3 грамма. И действительно, мать слизывает у них капельки мочи, которые в соответствии с игнобелевской моделью и не должны сами отделяться от канала.
По мнению авторов работы, их исследование — не просто удовлетворение любопытства; оно имеет практическую значимость. Во-первых, многие нарушения мочеиспускания изучают на животных, и теперь в руках медиков есть надежный инструмент для масштабирования полученных данных, чтобы их можно было применять к человеку. А во-вторых, бионический принцип позволит инженерам лучше проектировать масштабируемые гидродинамические системы, ведь мочевой пузырь и связанный с ним канал ничем не отличается от какого-нибудь нефтехранилища, привязанного к нефтепроводу.
Теперь же аналогичную модель удалось создать для объяснения феномена дефекации. Действуя по схожей методике, исследователи из лаборатории доцента Ху определили: у подавляющего большинства млекопитающих, у которых твердые отходы жизнедеятельности выходят единым куском, а не орешками, как у коз или зайцев, имеется свой инвариант: этот процесс в норме (то есть без расстройства кишечника) занимает 12 секунд вне зависимости от веса животного. При этом скорость дефекации пропорциональна кубическому корню из веса. То есть длине животного, поскольку последняя также пропорциональна этому корню. Соответственно статистическая обработка данных измерения показывает, что время дефекации очень слабо зависит от веса — в степени -0,09, то есть чем больше вес, тем меньше время опорожнения, хотя 40-сантиметровая прямая кишка слона в десять раз длиннее, чем у кота.
 |
|
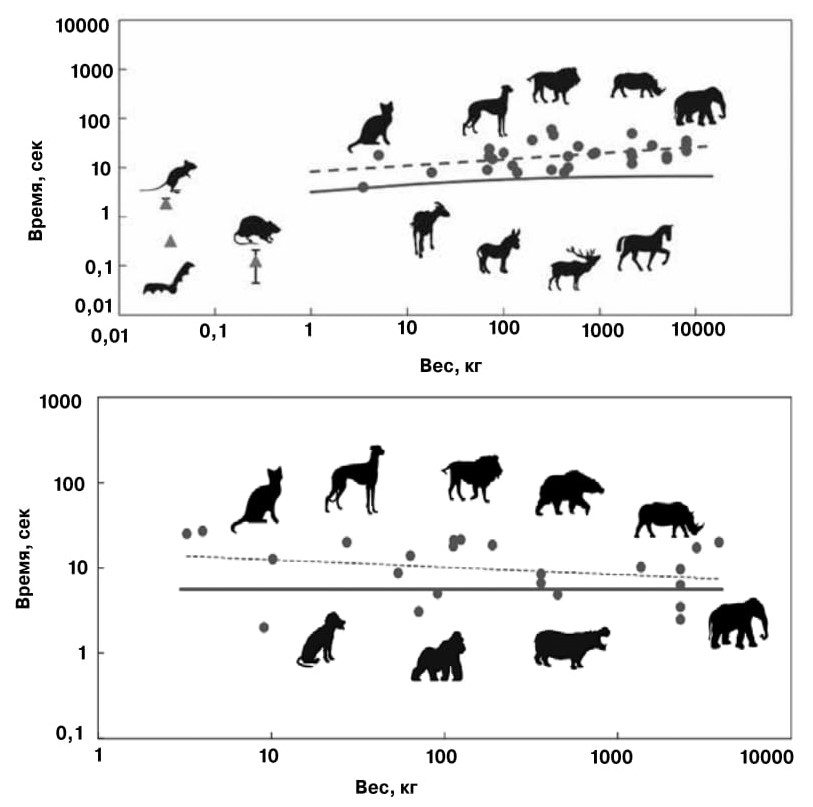
Время освобождения животного от жидких (вверху) и твердых (внизу) отходов жизнедеятельности почти не зависит от веса тела («Proceedings of the National Academy of Science», 2014, 11, 38 и «Soft Matter» 25 апреля 2017 года соответственно) |
Причиной такой инвариантности служит подобный найденному в первой работе набор физиологических констант и зависимостей, связывающих некие размеры с массой тела. В данном случае фундаментальной константой для всех млекопитающих стало минимальное давление, оказываемое гладкими мышцами кишечника на выделение в процессе дефекации, — 0,64 кПа; максимальное давление — в семь раз больше. С массой же тела связаны такие геометрические параметры, как диаметр и длина прямой кишки, а также толщина слизи на ее стенках: все они пропорциональны кубическому корню от веса. Интересно, что давление оказалось меньше, чем модуль сдвига твердых испражнений, который находится в пределах от 2 кПа у поссума до 10 кПа у овцы. Иными словами, деформироваться в процессе выхода они не могут, отчего важнейшее значение в кинематике процесса приобрела слизь — она играет роль смазки, и от нее зависит все.
Подстановка в формулу для времени дефекации всех зависимостей привела к тому, что показатели степеней при весе сократились, то есть время стало пропорционально весу в степени 0 — это оказался истинный инвариант, не то что время деуринации, которое от веса все-таки немного зависит. Однако подстановка значений дала время в 6,5 секунд, что в два раза меньше, нежели показал эксперимент. Такое несовпадение, видимо, связано с плохо изученными свойствами слизи. В самом деле, ту же ее толщину измеряли следующим образом: брали свежий экскремент, который из-за налипшей на нем слизи еще блестел, и взвешивали, а затем ждали, когда блеск исчезнет, и снова взвешивали, предполагая, что слизь испарилась и, значит, разница веса позволит посчитать толщину ее слоя. Такая методика конечно же не слишком точна. Еще большую ошибку могут вызвать неточные измерения вязкости этой слизи, ведь в формуле это не коэффициент, а показатель степени.
Впрочем, отсутствие количественного совпадения не препятствует верным качественным выводам. Так, было подсчитано время дефекации человека при поносе; оно оказалось очень малым — 0,5 секунды с момента приложения давления гладкими мышцами кишечника, движение же шло с ускорением, что очень похоже на правду. Интересный результат получился в обратной ситуации — при запоре. Исследователи предположили, что в рамках принятого приближения запор означает отсутствие слизи. В этом случае движение выдавливаемого материала возможно лишь в результате его сдвиговой деформации. Подстановка в расчетную формулу механических характеристик наиболее плотных испражнений дала колоссальное время для этого случая — 524 дня при минимальном давлении и 6 часов при максимальном. Поскольку был взят экстремальный случай — в реальности какая-то слизь обязательно будет, — эта ситуация качественно опять же оказалась недалека от реальности.
Таким образом, теперь, благодаря эпохальной серии работ группы доцента Ху, мы знаем о механике процессов удаления продуктов жизнедеятельности из организма практически все. Это дает возможность и врачам, и диетологам, рассуждая о путях улучшения жизни человечества, опираться не на слухи, домыслы и личное мнение, а на строгий научный инструментарий. Им теперь не надо пытаться играть с константами — их все равно не изменишь. А вот с переменными параметрами возможны варианты, которые и подлежат рассмотрению.
Фотохроники доцента Ху
Доцент Ху любит придумывать для своих студентов и аспирантов интереснейшие задания по гидродинамике и механике сплошных сред. Небезызвестное исследование пролета комара сквозь капли дождя (см. «Химию и жизнь», 2012, 7) выполнили его подопечные. В числе прочих интересных тем — гидродинамика потока муравьев и их агломерация в непромокаемые маты в случае наводнения, использование лягушкой вязкоупругого языка и неньютоновской слизи для ловли мух или бег насекомых по поверхности воды как демонстрация силы поверхностого натяжения. Так, водомерки возбуждают своими лапками диполярные вихри, что можно выявить с помощью красителя. Поскольку в штат лаборатории входят профессиональные фотографы, эти исследования всегда сопровождаются прекрасными фотографиями, которые можно посмотреть на сайте лаборатории www.hu.gatech.edu

